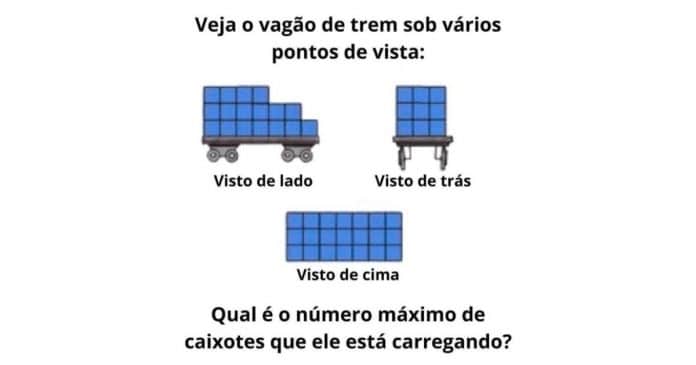
Você já parou para pensar como diferentes perspectivas podem mudar completamente a forma como enxergamos uma situação?
Recentemente, um desafio viral tem chamado a atenção nas redes sociais exatamente por isso: ele mostra um vagão de trem carregando caixotes e pede que o observador descubra o número máximo de caixotes transportados.
Dessa maneira, você deve analisar as imagens de três ângulos diferentes: lado, trás e cima.
Parece simples? Nem tanto. Vamos analisar juntos!
Entendendo o desafio
A imagem apresenta o vagão sob três pontos de vista:
- Vista de lado: revela a quantidade de caixotes em camadas, com diferentes alturas ao longo do comprimento do vagão.
- Vista de trás: mostra como estão dispostos os caixotes em profundidade.
- Vista de cima: indica o número de caixotes distribuídos na base do vagão.
A pergunta é direta: Qual é o número máximo de caixotes que o vagão pode estar carregando?
Analisando cada vista
Vista lateral
Observando o vagão de lado:
- Existem 7 colunas de caixotes.
Dessas 7 colunas:
- 4 colunas têm 3 caixotes empilhados.
- 2 colunas têm 2 caixotes empilhados.
- 1 coluna tem 1 caixote apenas.
Vista traseira
Na visão de trás:
- Há 3 colunas de caixotes.
- Cada coluna tem 3 caixotes empilhados.
Vista de cima
Na visão superior:
- Observam-se 7 colunas de caixotes.
- Cada coluna contém 3 caixotes.
Essas informações nos ajudam a entender como os caixotes estão distribuídos dentro do vagão.
Como calcular o número máximo de caixotes?
Agora, com as informações corretas:
Vista de cima: mostra que existem 7 × 3 = 21 posições ocupadas.
Para cada posição, a quantidade de caixotes empilhados é definida pelas alturas vistas de lado e de trás:
Pelos dados da vista lateral, sabemos quantas alturas existem em cada coluna.
Pela vista de trás, confirmamos que a altura máxima é de 3 caixotes.
Assim:
Temos 21 posições no topo.
A altura das pilhas varia entre 1, 2 ou 3 caixotes.
Combinando tudo:
4 colunas (com 3 posições cada) têm 3 caixotes empilhados:
- 4×3×3= 36 caixotes
2 colunas (com 3 posições cada) têm 2 caixotes empilhados:
- 2×3×2=12 caixotes
1 coluna (com 3 posições) tem 1 caixote apenas:
- 1×3×1=3 caixotes
Resultado final
Somando tudo:
36+12+3=51 caixotes
Portanto, o número máximo de caixotes que o vagão está carregando é 51!
Esse desafio fará com que você treine seu raciocínio lógico visual e espacial. No entanto, não basta olhar superficialmente, é necessário combinar todas as perspectivas para montar a estrutura completa.


